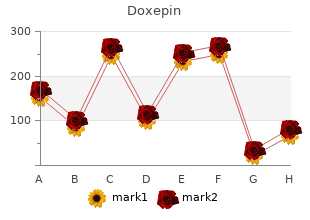
Brooks Institute. O. Thorek, MD: "Buy Doxepin online no RX - Safe online Doxepin no RX".
Be- cause of the generally complicated mathematical treatment required by complex 130 G order doxepin overnight anxiety network. Berger equations doxepin 10 mg on-line anxiety symptoms psychology, the final step will be the numerical resolution of these equations on a computer generic 10 mg doxepin with visa anxiety nervousness. We may observe that this resolution, based on the rigorous methods of numerical analysis, occurs only in the terminal phase of the modeling process. In the best case, these neurons correspond to a preliminary discretization of space. If each neuron is an elementary circuit, then discretization is done at each point in space where a given neuron exists. In contrast, with mathematical modeling, the resolution of equations is carried out in a continuous space, and discretization does not depend on the position of neurons, only on the mathematical constraints of resolution. However, as we will see, with more complicated models, only the mathematical approach is appropriate. Indeed, mathematical modeling does more than establish relationships between observables. In a correctly adapted representation, not only simplifications, but also a certain type of organization, a functional order, may appear. Determining the space, that is, the eigenvectors, in which a matrix is trans- formed into a diagonal matrix (in which only the diagonal numbers, the eigenvalues, are not null) puts the response of the system in a direct relationship to the input. By using this mathematical transformation, the state variables are kept distinct. There is a decoupling in the subsystems, each of them being represented by a single state vari- able. Similarly, when the matrix is reduced to diagonal blocks, several state variables describe the subsystem. As we see in this simple case, the new representation has led to new properties for the couplings between subsystems. More generally, with this type of representation we may obtain a new interpretation and discover new properties specific to the phe- nomenon observed. We have chosen hierarchical structural and functional representations, which pro- vide new laws for the functional organization of biological systems. Because the formulation calls for complex mathematical techniques, the equations have been grouped in appendices. Here, the interested reader will find part of the mathematical reasoning behind the theory. Two kinds of neural networks, artificial and real, will be presented first, followed by the theoretical framework. In the concluding section, we discuss the technique appropriate for neuromimetic circuits. Mathematical Modeling of Neuromimetic Circuits 131 What Is an Artificial Neural Network? The field of artificial neural networks has been extensively developed in the past few years. Each artificial neuron is a mathematical entity possessing two properties: (1) the output Y is the sum of the inputs Xi, weighted by the synaptic e‰cacies mi; and (2) the variation of the synaptic e‰cacy is proportional to the input signal Xi and the output signal Y. In the case of a network of n neurons connected to a given neuron, these properties are mathematically represented by a nonlinear dynamic system: " Xn Y ¼ F miXi i¼1 ð7:1Þ dmi ¼ aiX Yi ; i ¼ 1;... The second equation of this system is known as the learning rule of the neural network. With a given connectivity between neurons, the problem is to determine the math- ematical properties of the network related to the learning and memorization of pat- terns. All these net- works possess specific mathematical properties that unfortunately do not correspond to biological reality. Another di‰culty arises from the nonlinearity of the mathematical systems and the impossibility of finding an analytical solution for a dynamic system involving synap- tic weighting. The true complexity of the problem will be readily appreciated when we consider that the artificial neuron and its corresponding network are extremely simple compared with the real neuron surrounded by nervous tissue. From the biological point of view, the complexity of the phenomena involved is es- sentially the same whether we consider a real, isolated neuron or a network of artifi- cial neurons. This idea stimulated the search for a representation incorporating the properties of a real neural network (G. Over the past few years, much headway has been made in the mathematical description of a real biological 132 G. The hierarchical organization of biological structural units from the cellular to the organismal levels (cell organelles, nuclei, neurons, synapses, neural groups, nervous tissue, and cerebral organs), naturally suggested a hierarchical representa- tion of a system. However, the hierarchical aspect of the corresponding functional organization is far from evident. The novel three-dimensional representation of a biological system that one of us has proposed (G. Chauvet, 1996a), with axes for space scales, time scales, and structural units, allows visualization of the coupling between the structural and functional organizations. This representation is based es- sentially on the determination of the time scales of the dynamic systems describing physiological functions. This functional hierarchy is useful for determining the phys- iological functions associated with nervous structures. In the case of real neural net- works, there are at least two physiological functions: the propagation of membrane potential on a time scale on the order of milliseconds, and the modification of synap- tic e‰cacy on a time scale on the order of seconds or even hours. Thus, the func- tional order has its origin in a functional hierarchy that is evidently a manifestation of molecular mechanisms. Typically, the artificial neural networks generally studied have several neuron layers. The structure-function rela- tionship is more evident in this representation than in any other one. The hierarchical network is fundamentally di¤erent and, in particular, possesses specific emergent properties, that is, properties that appear at a higher level in a new structure. An im- Inputs Outputs (behaviors) Sensory Hierarchical Motor neurons circuit neurons Figure 7. Properties emerge from a lower level and appear at a higher level inside a new structure. This new structure is called a functional unit if, and only if, it has a specific function. Mathematical Modeling of Neuromimetic Circuits 133 portant advantage of the hierarchical representation is that it o¤ers a rigorous ap- proach to the notion of a functional unit that may now be defined as a structural unit with a specific function at a higher level of organization (G. The functional unit, possessing its own time scale, incorporates a new function that can be derived mathematically from the lower levels of organization in a biological system.
High-risk patients include newborns buy doxepin with visa anxiety symptoms but not anxious, the debilitated purchase generic doxepin pills anxiety symptoms dsm, and the tive mechanisms allow survival of the aspirated organisms cheap doxepin 75mg with mastercard anxiety eating disorder. The organisms cause gastroenteritis, typhoid bloodstream of people with severe illnesses and conditions such as fever, septicemia, and a severe, sometimes fatal type of food poi- neutropenia, the host is unable to mount adequate defenses and sep- soning. Humans become infected through ingestion of contaminated organisms causing nosocomial septic shock and meningitis. Infection by food usually strain, called O157:H7, causes hemorrhagic colitis, a disease char- results from ingestion of contaminated meat or by hands transfer- acterized by severe abdominal cramps, copious bloody diarrhea, ring organisms from an infected source. In the United States, and hemolytic-uremic syndrome (hemolytic anemia, thrombo- undercooked poultry and eggs are common sources. Hemolytic-uremic syndrome Salmonella enterocolitis is a common cause of food-borne out- occurs most often in children. Diarrhea usually begins several hours intestinal tract of animals, especially cattle, and several epidemics after ingesting contaminated food and may continue for several have been associated with ingestion of undercooked ground beef. Other sources include contaminated water and milk and person-to- Shigella person spread. Because it cannot survive in nature, the presence of Shigella species cause gastrointestinal problems ranging from E. Humans, who seem to Klebsiella be the only natural hosts, become infected after ingestion of con- Klebsiella organisms, which are normal bowel flora, may infect the taminated food or water. Effects of shigellosis are attributed to the respiratory tract, urinary tract, bloodstream, burn wounds, and loss of fluids, electrolytes, and nutrients and to the ulceration that meninges, most often as opportunistic infections in debilitated per- occurs in the colon wall. In pneumococcal penicillin use because the organisms produced beta-lactamase en- infections resistant to penicillins and cephalosporins, vancomycin, zymes (penicillinases) that destroyed penicillin. To decrease one of five drugs developed to resist the action of beta-lactamase spread of resistant S. MRSA have an • Pneumococcal vaccination for people older than 2 years of additional PBP called 2a or 2′. Methicillin cannot bind effectively age with increased risk of pneumococcal infection, and for to the PBPs and inhibit bacteria cell wall synthesis except with very all people older than 65 years of age. Consequently, minimum inhibitory con- Vancomycin-Resistant Enterococci centrations (MICs) of methicillin increased to high levels that were Enterococci have intrinsic and acquired resistance to many anti- difficult to achieve. For example, penicillins and cephalosporins inhibit the term MRSA is commonly used but misleading because rather than kill the organisms at achievable concentrations, and the organisms are widely resistant to penicillins (including all of aminoglycosides are ineffective if used alone. As a result, standard the antistaphylococcal penicillins, not just methicillin) and treatment of an enterococcal infection outside of the urinary tract has cephalosporins. Many strains of MRSA are also resistant to eryth- involved a combination of ampicillin and gentamicin or strepto- romycin, clindamycin, tetracycline, and the aminoglycosides. This combination is often successful because the ampicillin MRSA frequently colonize nasal passages of health care workers and damages the bacterial cell wall and allows the aminoglycoside are increasing as a cause of nosocomial infections, especially in crit- to penetrate the bacterial cell. In addition, the incidence of methicillin-resistant vancomycin is given with an aminoglycoside. The incidence of multidrug-resistant enterococci and MRSE is that vancomycin is the drug of choice for treatment. Two major types (Van A and However, vancomycin has been used extensively to treat infections Van B) of VRE have been described, with different patterns of anti- caused by S. Van B is susceptible to teicoplanin; Van A tance is increasing in those species. Because resistance genes from is resistant to teicoplanin but may be susceptible to minocycline, the other organisms can be transferred to S. Vancomycin-resistant enterococci A major contributing factor to VRE is increased use of van- (VRE) are discussed later. Therefore, to decrease the spread of VRE, cal infections (eg, community-acquired pneumonia, bacteremia, the CDC recommends limiting the use of vancomycin. However, penicillin- recommendations include avoiding or minimizing use in routine resistant strains and multidrug-resistant strains are being identified surgical prophylaxis, empiric therapy for febrile patients with neu- with increasing frequency. Risk factors for the development of tropenia (unless the prevalence of MRSA or MRSE is high), sys- resistant strains include frequent antibiotic use and prophylactic temic or local prophylaxis for intravascular catheter infection or antibiotics. Children in day care centers are often colonized or infected antibiotic-associated colitis, and routine prophylaxis for very with antibiotic-resistant S. This is attributed to a high low birth weight infants or patients on continuous ambulatory incidence of otitis media, which is often treated with a penicillin peritoneal dialysis. Resistant strains in adults and elderly clients are cleaning are also important because VRE can survive for long often associated with previous use of a penicillin or cephalosporin periods on hands, gloves, stethoscopes, and environmental sur- and hospitalization. Stetho- by decreasing the ability of their PBPs to bind with penicillin scopes should be used only with an infected patient or cleaned (and other beta-lactam antibiotics). Organisms displaying high- thoroughly between patients if used for both VRE-infected and level penicillin resistance may be cross-resistant to second- and uninfected patients. CHAPTER 33 GENERAL CHARACTERISTICS OF ANTIMICROBIAL DRUGS 499 by immunosuppressive disorders or drugs. They may emerge ally, resistant bacterial strains of major concern include during or after antimicrobial drug therapy. Contributing fac- penicillin-resistant Streptococcus pneumoniae, methicillin- tors include: resistant Staphylococcus aureus and Staphylococcus epi- 1. Widespread use of antimicrobial drugs, especially dermidis, vancomycin-resistant enterococcus, and multidrug- broad-spectrum agents. Actually, all of these for which they are prescribed, transient organisms, other organisms are resistant to multiple antibiotics. When the normal flora is are described in Box 33–2; MDR-TB is discussed in Chapter suppressed, space and nutrients become available to sup- 38. Viruses and fungi also develop resistance to antimicrobial port the growth of organisms resistant to the effects of drugs, as discussed in Chapters 39 and 40. Once established, resistant bacteria Mechanisms of Resistance can cause superinfection in the original host, spread to other hosts, and even spread their resistance properties Bacteria have developed numerous ways to acquire resis- for that antibiotic to other species of bacteria. In addi- tance to antimicrobial drugs, including: tion to resistance to the effects of one antibiotic, cross- • Production of enzymes that inactivate the drugs. For ex- resistance to similar antibiotics also occurs because ample, beta-lactamase enzymes change the chemical most antibiotics are variations of a few basic types. Interrupted or inadequate antimicrobial treatment the beta-lactam ring and preventing the antibiotic from of infections. Clients often stop taking a prescribed anti- binding with its target site (called penicillin-binding biotic when symptoms subside or they feel better. Gram-negative bacteria • Changing their cell walls to produce porins that prevent associated with high rates of antibiotic resistance include penetration of the drug. Pseudomonas aeruginosa and Serratia, Enterobacter, • Acquiring the ability to pump drug molecules out of the and Acinetobacter species. Multiple, nonspecific efflux systems become acti- ently resistant to penetration of antibiotics and acquire vated to remove foreign chemicals. One mechanism is • Transferring genetic material (DNA or plasmids) be- an outer membrane with openings (porins) that regu- tween microorganisms. Some gram-negative bacte- nisms for genetic exchange that allow them to spread ria (eg, E.